WikiSort.ru - Программирование

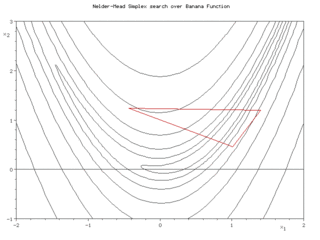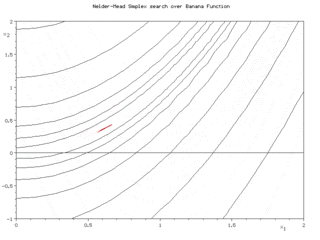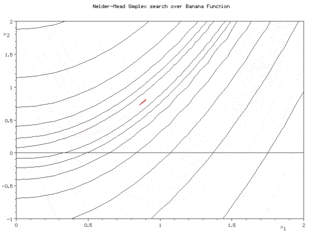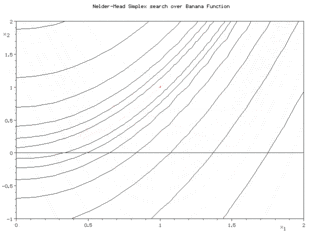
Последовательные симплексы в методе Нелдера-Мида для функции Розенброка (вверху) и функции Химмельблау (внизу)

Не путать с «симплекс-методом» из линейного программирования — методом оптимизации линейной системы с ограничениями.

Метод Нелдера — Мида, также известный как метод деформируемого многогранника и симплекс-метод, — метод безусловной оптимизации функции от нескольких переменных, не использующий производной (точнее — градиентов) функции, а поэтому легко применим к негладким и/или зашумлённым функциям.

Суть метода заключается в последовательном перемещении и деформировании симплекса вокруг точки экстремума.

Метод находит локальный экстремум и может «застрять» в одном из них. Если всё же требуется найти глобальный экстремум, можно пробовать выбирать другой начальный симплекс. Более развитый подход к исключению локальных экстремумов предлагается в алгоритмах, основанных на методе Монте-Карло, а также в эволюционных алгоритмах.

Алгоритм

Пусть требуется найти безусловный минимум функции n переменных ${\displaystyle f\left(x^{(1)},x^{(2)},\ldots ,x^{(n)}\right)}$ . Предполагается, что серьёзных ограничений на область определения функции нет, то есть функция определена во всех встречающихся точках.

Параметрами метода являются:

• коэффициент отражения ${\displaystyle \alpha >0}$ , обычно выбирается равным ${\displaystyle 1}$ .
• коэффициент сжатия ${\displaystyle \beta >0}$ , обычно выбирается равным ${\displaystyle 0{,}5}$ .
• коэффициент растяжения ${\displaystyle \gamma >0}$ , обычно выбирается равным ${\displaystyle 2}$ .

1. «Подготовка». Вначале выбирается ${\displaystyle n+1}$ точка ${\displaystyle x_{i}=\left(x_{i}^{(1)},x_{i}^{(2)},\ldots ,x_{i}^{(n)}\right),i=1..n+1}$ , образующие симплекс n-мерного пространства. В этих точках вычисляются значения функции: ${\displaystyle f_{1}=f(x_{1}),f_{2}=f(x_{2}),\ldots ,f_{n+1}=f(x_{n+1})}$ .
2. «Сортировка». Из вершин симплекса выбираем три точки: ${\displaystyle x_{h}}$ с наибольшим (из выбранных) значением функции ${\displaystyle f_{h}}$ , ${\displaystyle x_{g}}$ со следующим по величине значением ${\displaystyle f_{g}}$ и ${\displaystyle x_{l}}$ с наименьшим значением функции ${\displaystyle f_{l}}$ . Целью дальнейших манипуляций будет уменьшение по крайней мере ${\displaystyle f_{h}}$ .
3. Найдём центр тяжести всех точек, за исключением ${\displaystyle x_{h}}$ : ${\displaystyle x_{c}={\frac {1}{n}}\sum \limits _{i\neq h}x_{i}}$ . Вычислять ${\displaystyle f_{c}=f(x_{c})}$ не обязательно.
4. «Отражение». Отразим точку ${\displaystyle x_{h}}$ относительно ${\displaystyle x_{c}}$ с коэффициентом ${\displaystyle \alpha }$ (при ${\displaystyle \alpha =1}$ это будет центральная симметрия, в общем случае — гомотетия), получим точку ${\displaystyle x_{r}}$ и вычислим в ней функцию: ${\displaystyle f_{r}=f(x_{r})}$ . Координаты новой точки вычисляются по формуле:

   ${\displaystyle x_{r}=(1+\alpha )x_{c}-\alpha x_{h}}$ .

5. Далее смотрим, насколько нам удалось уменьшить функцию, ищем место ${\displaystyle f_{r}}$ в ряду ${\displaystyle f_{h},f_{g},f_{l}}$ .

   Если ${\displaystyle f_{r}<f_{l}}$ , то направление выбрано удачное и можно попробовать увеличить шаг. Производим «растяжение». Новая точка ${\displaystyle x_{e}=(1-\gamma )x_{c}+\gamma x_{r}}$ и значение функции ${\displaystyle f_{e}=f(x_{e})}$ .

   Если ${\displaystyle f_{e}<f_{r}}$ , то можно расширить симплекс до этой точки: присваиваем точке ${\displaystyle x_{h}}$ значение ${\displaystyle x_{e}}$ и заканчиваем итерацию (на шаг 9).

   Если ${\displaystyle f_{r}<f_{e}}$ , то переместились слишком далеко: присваиваем точке ${\displaystyle x_{h}}$ значение ${\displaystyle x_{r}}$ и заканчиваем итерацию (на шаг 9).

   Если ${\displaystyle f_{l}<f_{r}<f_{g}}$ , то выбор точки неплохой (новая лучше двух прежних). Присваиваем точке ${\displaystyle x_{h}}$ значение ${\displaystyle x_{r}}$ и переходим на шаг 9.

   Если ${\displaystyle f_{g}<f_{r}<f_{h}}$ , то меняем местами значения ${\displaystyle x_{r}}$ и ${\displaystyle x_{h}}$ . Также нужно поменять местами значения ${\displaystyle f_{r}}$ и ${\displaystyle f_{h}}$ . После этого идём на шаг 6.

   Если ${\displaystyle f_{h}<f_{r}}$ , то просто идём на следующий шаг 6.

   В результате (возможно, после переобозначения) ${\displaystyle f_{l}<f_{g}<f_{h}<f_{r}}$ .

6. «Сжатие». Строим точку ${\displaystyle x_{s}=\beta x_{h}+(1-\beta )x_{c}}$ и вычисляем в ней значение ${\displaystyle f_{s}=f(x_{s})}$ .
7. Если ${\displaystyle f_{s}<f_{h}}$ , то присваиваем точке ${\displaystyle x_{h}}$ значение ${\displaystyle x_{s}}$ и идём на шаг 9.
8. Если ${\displaystyle f_{s}>f_{h}}$ , то первоначальные точки оказались самыми удачными. Делаем «глобальное сжатие» симплекса — гомотетию к точке с наименьшим значением ${\displaystyle x_{l}}$ :

   ${\displaystyle x_{i}\gets x_{l}+(x_{i}-x_{l})/2}$ , ${\displaystyle i\neq l}$ .

9. Последний шаг — проверка сходимости. Может выполняться по-разному, например, оценкой дисперсии набора точек. Суть проверки заключается в том, чтобы проверить взаимную близость полученных вершин симплекса, что предполагает и близость их к искомому минимуму. Если требуемая точность ещё не достигнута, можно продолжить итерации с шага 2.

Источники

• КУРС «Многомерная оптимизация». Лекция 10. Метод Нелдера-Мида на сайте Института дистанционного обучения ИНТУИТ

. Подробное описание, есть иллюстрации.

• Метод Нелдера-Мида. Краткий алгоритм.
• Список ссылок на численные методы
• J.A. Nelder and R. Mead, Computer Journal, 1965, vol 7, pp 308—313 (текст не общедоступен) (англ.)